Technology & Innovation

Author: anonymDate: 2024-11-20 18:12:51

Experts Determine Optimal Method for Chart Navigation

Dijkstra’s algorithm was long thought to be the most efficient way to find a graph’s best routes. Researchers have now proven that it’s “universally optimal.”

This article initially appeared in Quanta Magazine. Regular travelers often believe they've found the most efficient route. However, 'optimal' is a subjective term. Unexpected events like accidents or road closures can dramatically alter travel times. This poses a significant challenge for developers of algorithms – the systematic processes computers use to solve problems. Numerous algorithms can achieve the same result, making the selection of the 'best' one incredibly difficult.

Consider, for example, an algorithm designed to identify the quickest path between two points. Many approaches can be devised to guarantee functionality. A successful algorithm must consistently determine the fastest route, regardless of location (London or Los Angeles) or time of day.

However, these algorithms vary in efficiency. The time required to compute the solution differs depending on context, and problems easily solved by one algorithm might be significantly more challenging for another. An algorithm consistently outperforming others is the ideal, though this is often unattainable. A recent breakthrough proves that for the classic route-finding problem, one algorithm approaches this ideal: Under the assumption of the worst possible traffic conditions, it's the superior method for any street layout. Remarkably, this algorithm is almost 70 years old and a mainstay of introductory computer science courses. This research will receive a best-paper award at next week's 2024 Symposium on Foundations of Computer Science. "It's extraordinary," stated Tim Roughgarden, a computer scientist at Columbia University. "I can't imagine a more impactful study on a problem we teach undergraduates."

Heaps and Bounds

This celebrated route-finding algorithm's story began with an unplanned diversion. In 1956, 26-year-old Dutch computer scientist Edsger Dijkstra aimed to create a program showcasing the capabilities of the new ARMAC computer. During a shopping trip with his fiancée in Amsterdam, he paused at a café. It was there that he conceived the algorithm bearing his name. Lacking writing materials, he meticulously formulated the details mentally over 20 minutes.

In a late-life interview, Dijkstra attributed the algorithm's enduring relevance to its unconventional origin. "Without pen and paper, you're practically forced to avoid unnecessary complexities," he remarked. Dijkstra's algorithm doesn't simply pinpoint the quickest route to a single destination; it provides a ranked list of travel times from the starting point to all possible destinations – addressing what researchers term the single-source shortest-paths problem. The algorithm operates on an abstract road map called a graph: a network of interconnected nodes (vertices) where connections between nodes are labeled with numbers (weights). These weights could represent travel times on a road network, and they are subject to change based on traffic conditions. Larger weights indicate longer travel times. To visualize Dijkstra's algorithm, picture traversing a graph, noting travel times from the origin to each new node. When facing a choice of direction, proceed toward the nearest unvisited node. If a quicker route to a node is discovered, update the time and discard the previous entry. Once the fastest path is identified, transfer the travel time to a separate, organized list.

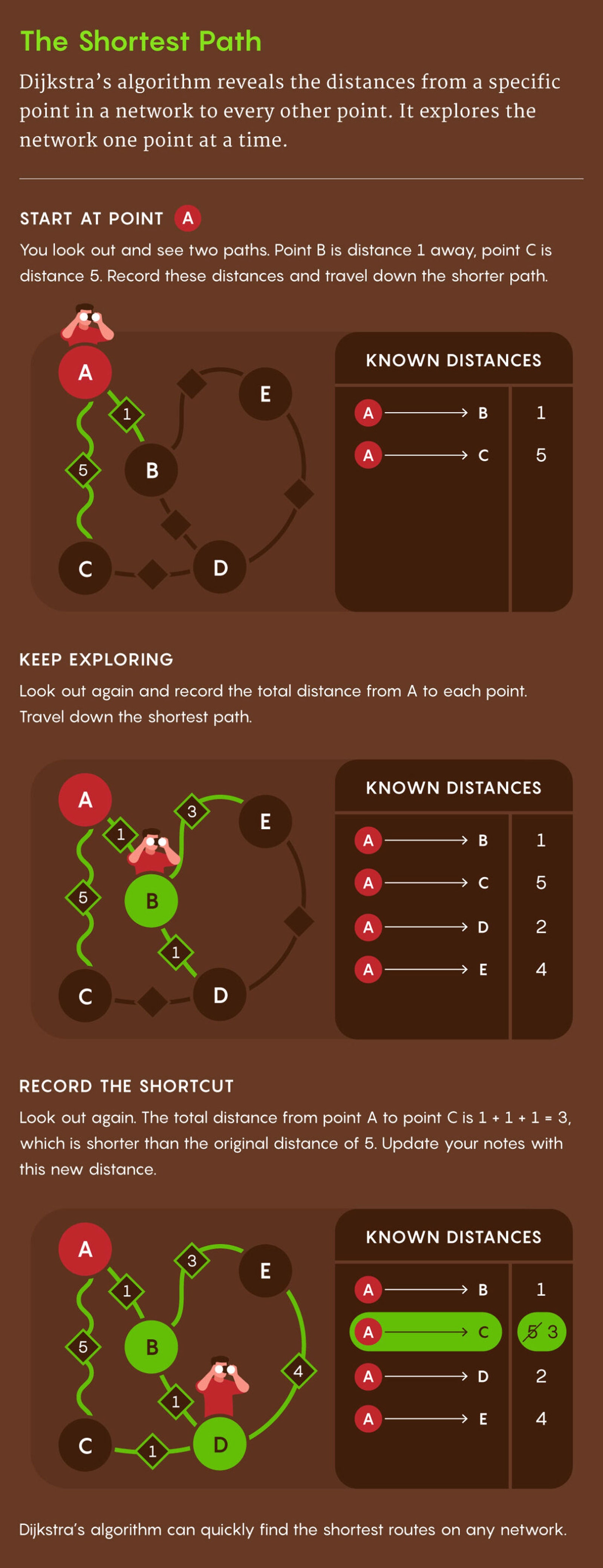
“It's a remarkable algorithm," said Erik Demaine, a computer scientist at the Massachusetts Institute of Technology. “It's exceptionally fast, straightforward, and easy to implement.” Practical implementation necessitates a system for managing notes – a data structure, in computer science jargon. This seemingly minor detail significantly impacts the algorithm's overall speed, as time spent searching through notes for edits or removals can be considerable. Dijkstra's original paper employed a basic data structure with room for improvement. Subsequently, researchers developed superior structures, affectionately termed "heaps," where specific entries are easily retrievable. These leverage the fact that Dijkstra's algorithm only needs to remove the entry for the closest unvisited node. "A heap is essentially a structure enabling rapid execution of this process," explained Václav Rozhoň, a researcher at the Institute for Computer Science, Artificial Intelligence and Technology (INSAIT) in Sofia, Bulgaria. In 1984, two computer scientists devised an ingenious heap design allowing Dijkstra's algorithm to reach a theoretical limit, or "lower bound," on the time needed to solve the single-source shortest-paths problem. In one specific sense, this version of Dijkstra's algorithm is optimal. This remained the final word on the standard problem for nearly 40 years. The situation evolved when researchers revisited the meaning of 'optimal'.

Best Behavior

Researchers typically evaluate algorithms by examining their performance in the worst-possible scenarios. Envision the world's most intricate street grid, complicated by extremely unpredictable traffic. If the objective is to locate the fastest routes under these extreme conditions, the 1984 version of Dijkstra's algorithm is undeniably superior. However, most cities lack such challenging layouts. This prompts the question: Is there an algorithm that excels in all road networks? The initial step is to make the conservative assumption of the worst-possible traffic conditions for every network. The algorithm should then determine the fastest paths through any network, even with the most unfavorable weights. Researchers call this condition "universal optimality." A universally optimal algorithm for the simpler problem of traversing a graph from one point to another could help navigate rush hour traffic in any city.

“This seems too good to be true,” commented Bernhard Haeupler, a computer scientist affiliated with INSAIT and the Swiss Federal Institute of Technology Zurich (ETH Zurich). Haeupler became engrossed in the potential of universal optimality while preparing a grant proposal in the mid-2010s. Many find this aspect of their work tedious, but Haeupler viewed it as an opportunity. "It allows you to disregard skepticism and simply envision the possibilities," he said. These visions materialized in 2021 when Haeupler and two graduate students proved the feasibility of constructing universally optimal algorithms for several critical graph problems. He hadn't considered whether the same was possible for the classic single-source shortest-paths problem. That would await a different graduate student with similar ambition.

The Shortest Path to Victory

In early 2023, Rozhoň was nearing the end of his graduate program at ETH Zurich. He had recently completed a paper on moving beyond worst-case analysis in a different context and was brainstorming new avenues of research with his co-author Jakub Tětek, then a graduate student at the University of Copenhagen. Rozhoň proposed attempting to develop a universally optimal algorithm for the single-source shortest-paths problem. "I said, 'No, that's impossible; it simply can't be done,'" Tětek recalled. But Rozhoň persuaded him to try. In the spring, the team expanded to three with the addition of Richard Hladík, a graduate student at ETH Zurich whom Rozhoň and Tětek had known since high school in the Czech Republic. The trio experimented with various aspects of Dijkstra's algorithm and its associated heap, managing to create a universally optimal version. However, the resulting algorithm was complex, and they couldn't identify the precise conditions necessary for universal optimality. This was insufficient in a field that values comprehensive and rigorous proof. The three students shifted their focus from mathematical to social networks. Rozhoň had begun discussing the problem with Haeupler while both were visiting colleagues in New York. From there, Haeupler flew to Panama for a vacation, but he couldn't fully disengage from the problem.

“It was truly a holiday,” he stated. “But even then, my thoughts didn't cease.”

During a video conference a few days into Haeupler's trip, the team of four adopted a new strategy, concentrating primarily on the choice of data structure. They soon suspected this would suffice – the rest of Dijkstra's algorithm could remain unchanged. Within a month, they had proven their hypothesis. The key turned out to be a specific property of some data structures allowing rapid access to recently added elements. Heaps with this property were first developed over 20 years ago, but their full potential remained untapped. The four researchers proved that only a data structure possessing this new property and all the features of the 1984 heap was necessary. The final step was its design. The last team member was Robert Tarjan, a computer scientist at Princeton University who co-invented the special 1984 heap. Tarjan, a Turing Award recipient (the field's highest honor), had mentored Haeupler in the late 2000s. When Tarjan visited Zurich in May, Haeupler invited him for fondue—his specialty—and mentioned the new shortest-paths project. Tarjan immediately agreed to participate.

The five researchers collaborated on creating a heap data structure with the required properties. They started with a cumbersome design, refining it incrementally until satisfied. "Each iteration allowed for simplification," Rozhoň noted. "I was surprised by its eventual simplicity." Some Dijkstra's algorithm variants have real-world applications in software like Google Maps. The new finding likely won't have similar practical uses, as numerous factors beyond theoretical optimality guarantees influence such applications. However, it might alter how researchers study optimality, encouraging a shift away from the typical worst-case analysis. Algorithms often achieve stronger guarantees at the cost of increased complexity. This new discovery suggests that simple algorithms with these stronger guarantees may be more prevalent than previously believed – the team has already identified two further instances. "The underlying concept is incredibly compelling," Tarjan stated. "The extent of its applicability remains to be seen."